Die vier Ziele bestehen aus kleinen flachen Platten, die bei 5,9 GHz für monostatische RCS bei einem Elevationswinkel von 10 Grad (über der Oberfläche der Platte) und unterschiedlichen Azimutwinkeln gemessen wurden. Die Ziele wurden von der NASA entwickelt und in [1] veröffentlicht. Die in diesem Beispiel verwendeten Messergebnisse wurden der späteren Veröffentlichung [2] entnommen.
Die Formen wurden auf der Grundlage verschiedener Faktoren ausgewählt, die für eine Simulationssoftware schwierig sind. Bei den Formen handelt es sich um eine "Visitenkarte", eine rechteckige Platte von 2 x 3,5 Wellenlängen, einen "Keilzylinder" mit einer dreieckigen und einer halbkreisförmigen Kante, die miteinander verbunden sind, einen "Plattenzylinder", der eine Kombination aus der Visitenkarte und der halbkreisförmigen Kante des Keilzylinders ist, und einen "Keilplattenzylinder", der eine Kombination aus den verschiedenen Formen darstellt. Die Abbildungen 1 - 4 zeigen die vier Formen. [Hinweis: Ausführlichere Erläuterungen zu jeder der in diesem Beispiel verwendeten Figuren finden Sie weiter unten.] Für die Simulationen wurde angenommen, dass die Platten eine Dicke von 41 mils haben und perfekt leitend sind.
Abbildung 1: Die Geometrie der Visitenkarte.
Abbildung 2: Die Geometrie des Keilzylinders.
Abbildung 3: Die Geometrie des Plattenzylinders.
Abbildung 4: Die Geometrie des Keilplattenzylinders.
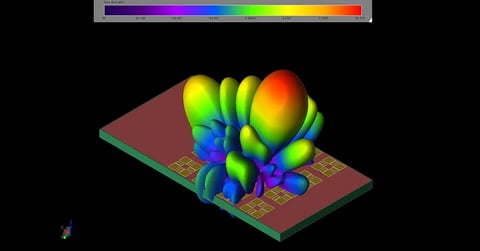
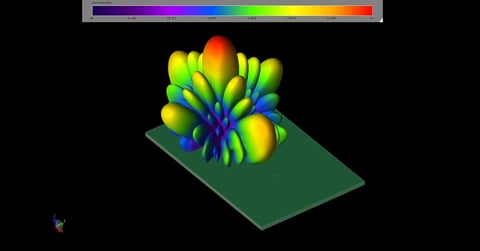
Die Simulationen wurden mit XFdtd durchgeführt, wobei die XACT-Vernetzungsfunktion für alle Ziele außer der "Visitenkarte" verwendet wurde. Die Software verwendete für alle Simulationen eine Maschengröße, die 20 Zellen pro Wellenlänge bei der Zielfrequenz (5,9 GHz) entspricht, und die Festpunktfunktion wurde für alle Geometrien verwendet. In einigen Fällen waren gute Ergebnisse mit einer geringeren Auflösung möglich, aber aus Gründen der Konsistenz werden alle Ergebnisse in derselben Auflösung dargestellt. Zur besseren Veranschaulichung der Simulationstreue ist in Abbildung 5 ein Blick auf das Netz für die Keilplatten-Zylinder-Geometrie zu sehen.
Abbildung 5: Eine dreidimensionale Ansicht des geometrischen Netzes des Keilplattenzylinders.
Bei den Simulationen wurde eine einfallende ebene Welle mit einer sinusförmigen Quelle verwendet, und die Daten wurden mit einer stationären Fernzonentransformation erfasst. Es hat sich gezeigt, dass diese Kombination die schnellsten Ergebnisse für diese Einzelfrequenzanalyse liefert. Aufgrund der in einer Rückstreu-RCS-Situation erforderlichen Ergebnisse ergab jede Simulation einen einzigen Datenpunkt für die Dateiausgabegrafik.
Die XStream-GPU-Lösung wurde zur Durchführung aller Simulationen verwendet, um die schnellsten Ergebnisse zu erzielen. Es wurde ein Parameter-Sweep mit einem einzigen Wert durchgeführt, wobei die Einfallsrichtung phi (Azimutwinkel) als Parameter in Schritten von einem Grad verwendet wurde. Die Ausgabe wurde mit einem benutzerdefinierten Skript verarbeitet, um das Rückstreu-RCS bei jedem Einfallswinkel zu extrahieren und die Ergebnisse in einem einzigen Diagramm darzustellen. Für jeden Einfallswinkel wurden weniger als 20 Sekunden Ausführungszeit auf einer NVIDIA Quadro FX 1600M Grafikkarte benötigt.
Die Geometrie der Visitenkarte ist bereits auf das rechteckige FDTD-Gitter ausgerichtet, so dass die Verwendung der XACT-Vernetzungsfunktionen nicht erforderlich war. Die Geometrie ist so ausgerichtet, dass der Azimut 0 Grad normalerweise auf eine der kürzeren Seiten der Platte fällt. Die simulierten Ergebnisse im Vergleich zu den gemessenen Ergebnissen aus den referenzierten Veröffentlichungen sind in den Abbildungen 6 und 7 für die vertikale bzw. horizontale Polarisation dargestellt. Die Ergebnisse zeigen im Allgemeinen eine gute Übereinstimmung über alle Einfallswinkel. Die etwas niedrigeren simulierten RCS-Werte für die Mitte der vertikalen Polarisationskurve spiegeln die simulierten Ergebnisse wider, die auch von den Autoren der referenzierten Veröffentlichungen vorgelegt wurden.
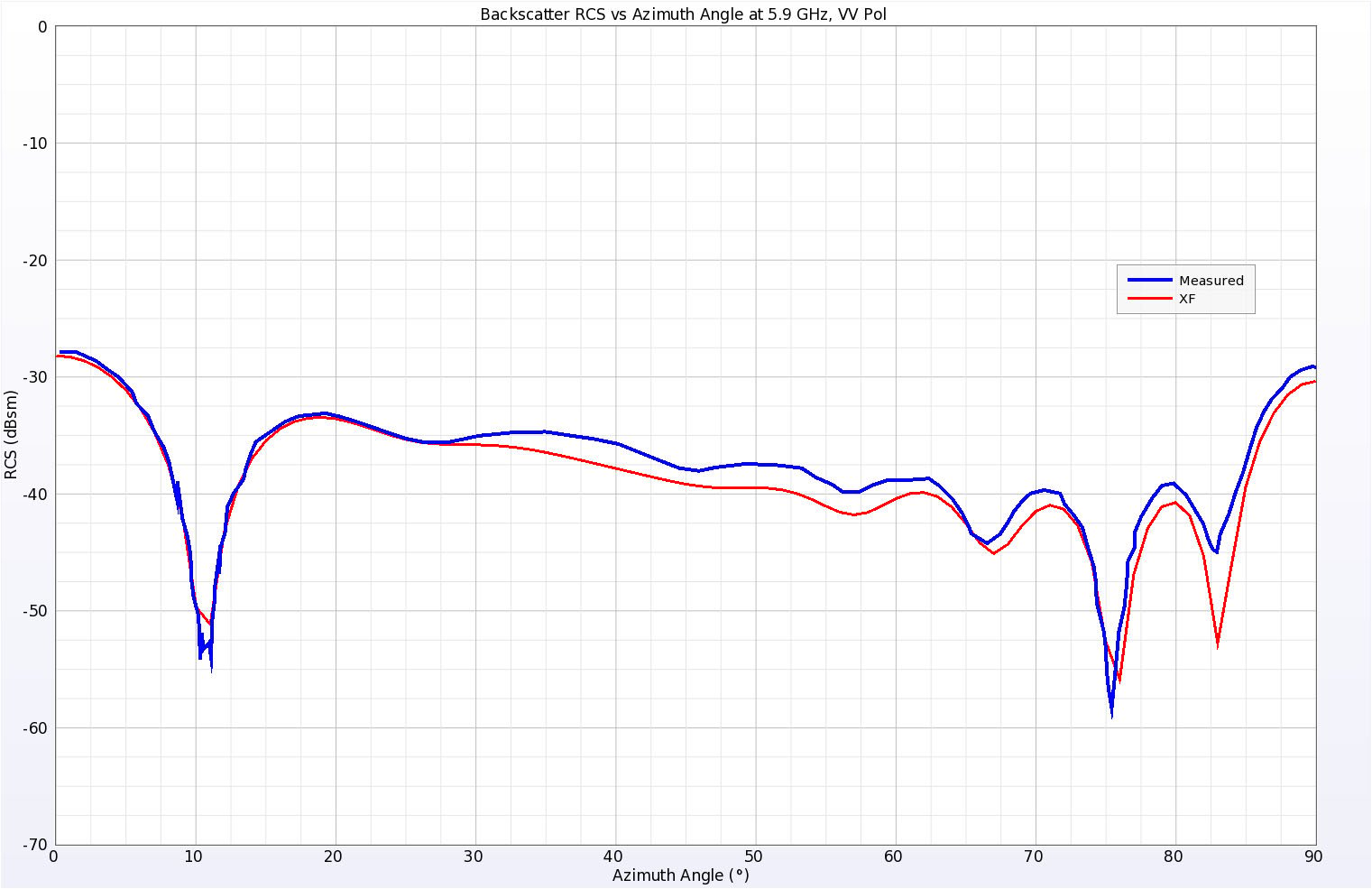
Abbildung 6: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für die Visitenkarte bei 5,9 GHz, vertikale Polarisation.
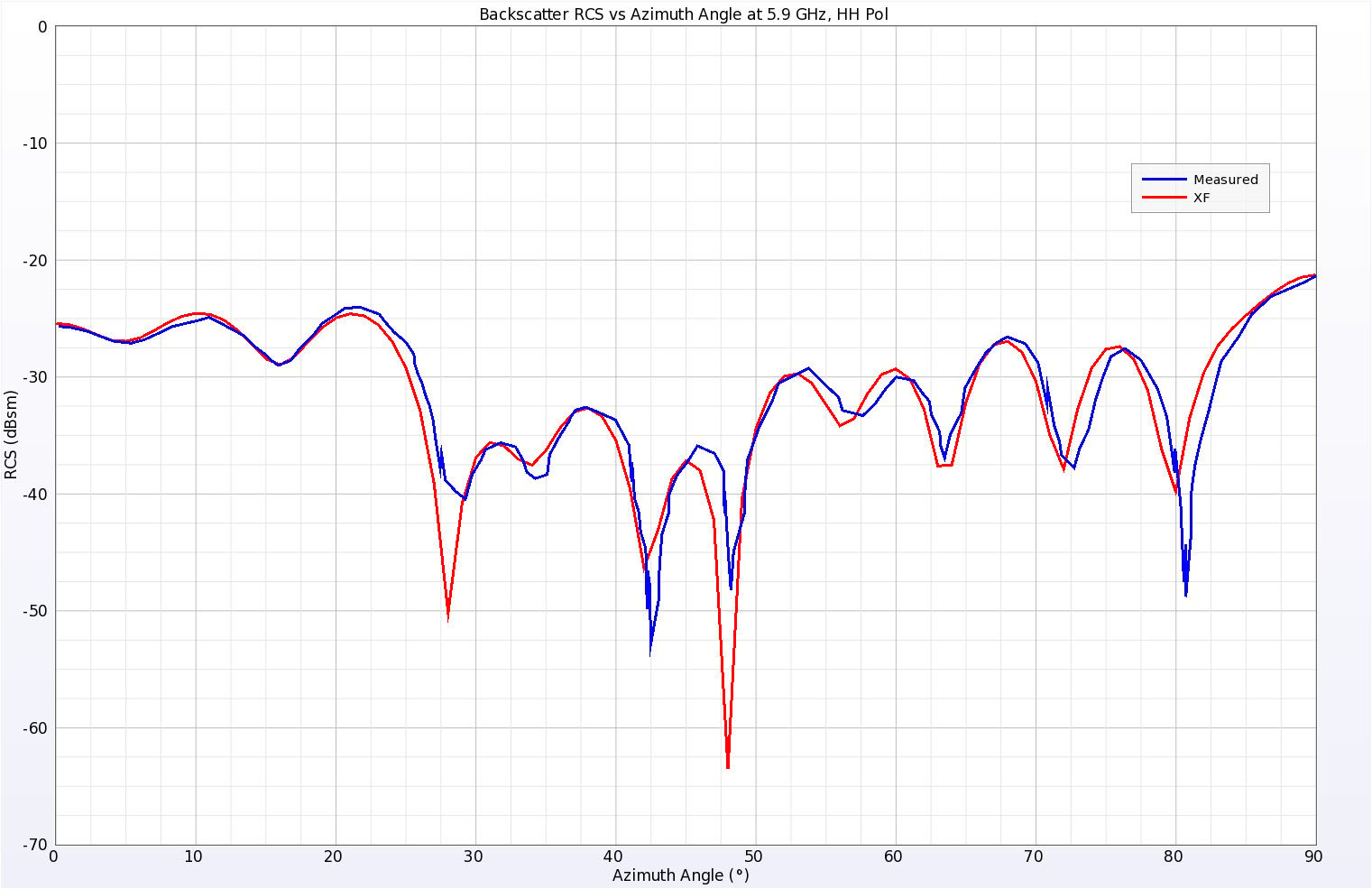
Abbildung 7: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für die Visitenkarte bei 5,9 GHz, horizontale Polarisation.
Der Keilzylinder stellt aufgrund der gekrümmten Oberflächen und der scharfen Spitze eine größere Herausforderung für die FDTD-Simulation dar. In der XFdtd-Simulation wurde am Scheitelpunkt des Keils ein fester Punkt hinzugefügt, um sicherzustellen, dass ein ausgewogenes Netz erstellt wurde. Die RCS-Ergebnisse für beide Polarisationen sind in den Abbildungen 8 und 9 dargestellt und stimmen im Allgemeinen gut mit den veröffentlichten Messungen überein.
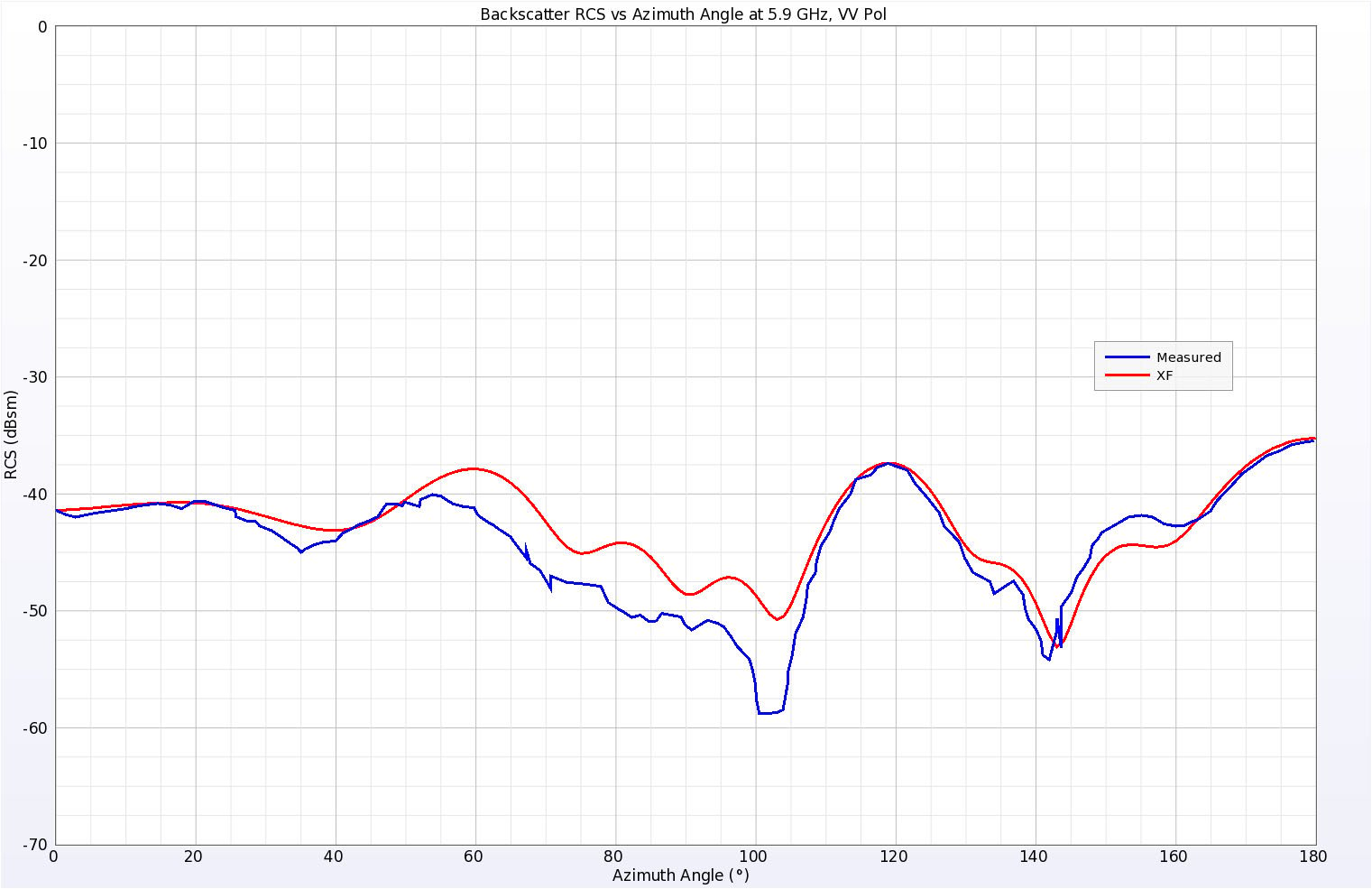
Abbildung 8: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für den Keilzylinder bei 5,9 GHz, vertikale Polarisation.
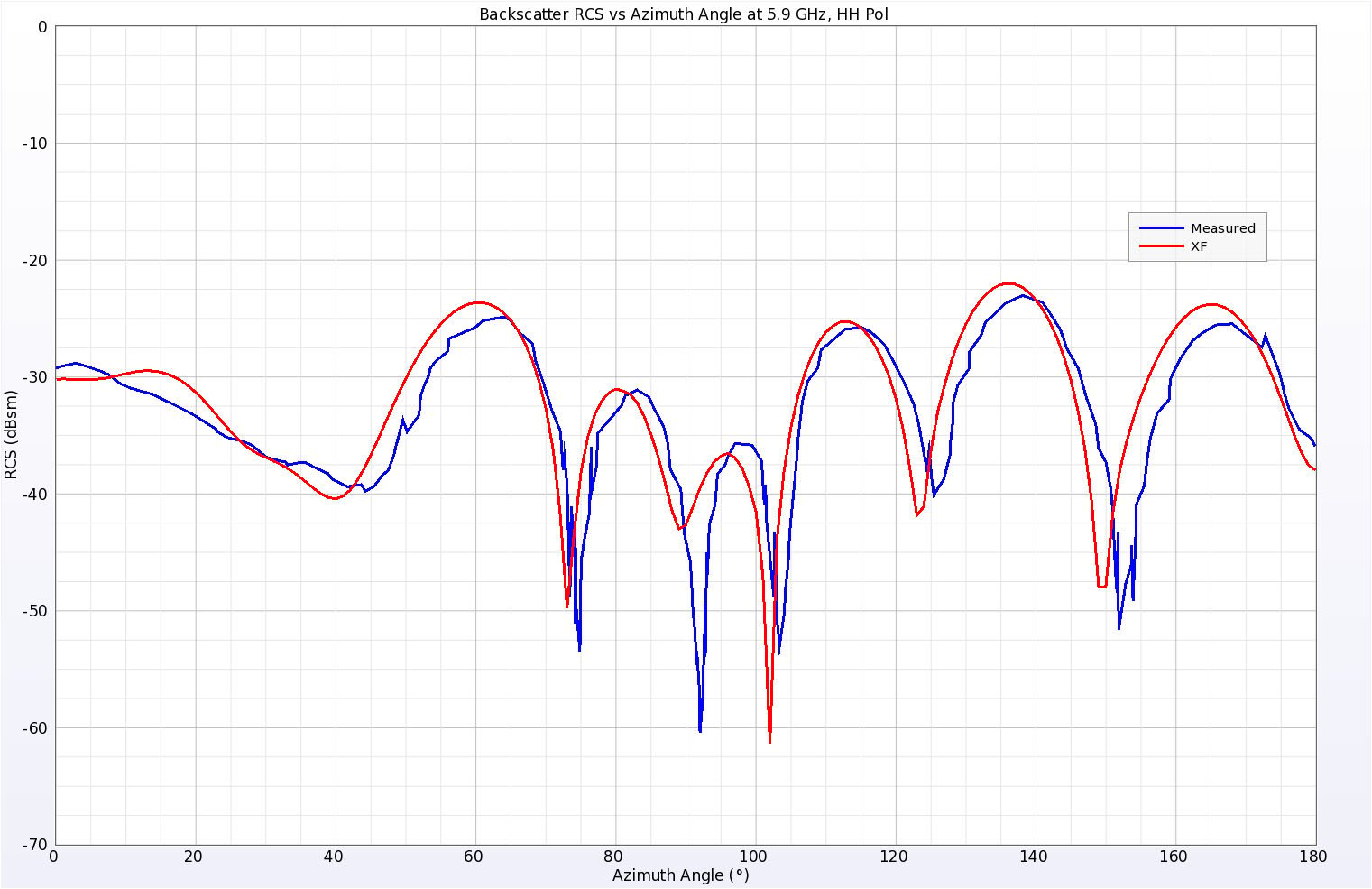
Abbildung 9: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für den Keilzylinder bei 5,9 GHz, horizontale Polarisation.
Die Geometrie des Plattenzylinders basiert auf der Form der Visitenkarte, fügt aber einen halbkreisförmigen Teil an einer der kurzen Seiten hinzu. Die simulierten Ergebnisse stimmen wiederum gut mit den gemessenen Ergebnissen überein, wie in den Abbildungen 10 und 11 zu sehen ist.
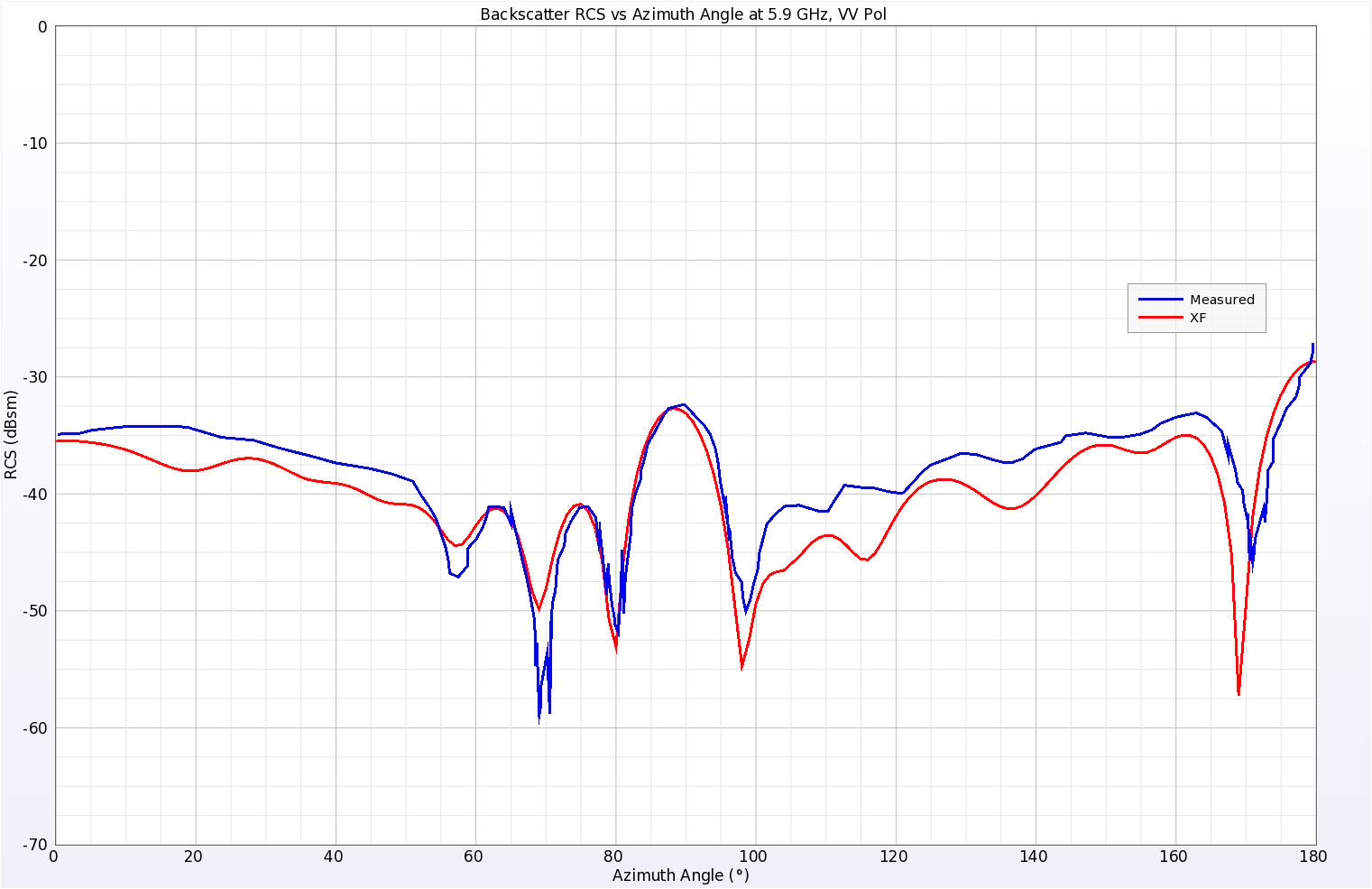
Abbildung 10: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für den Plate Cylinder bei 5,9 GHz, vertikale Polarisation.
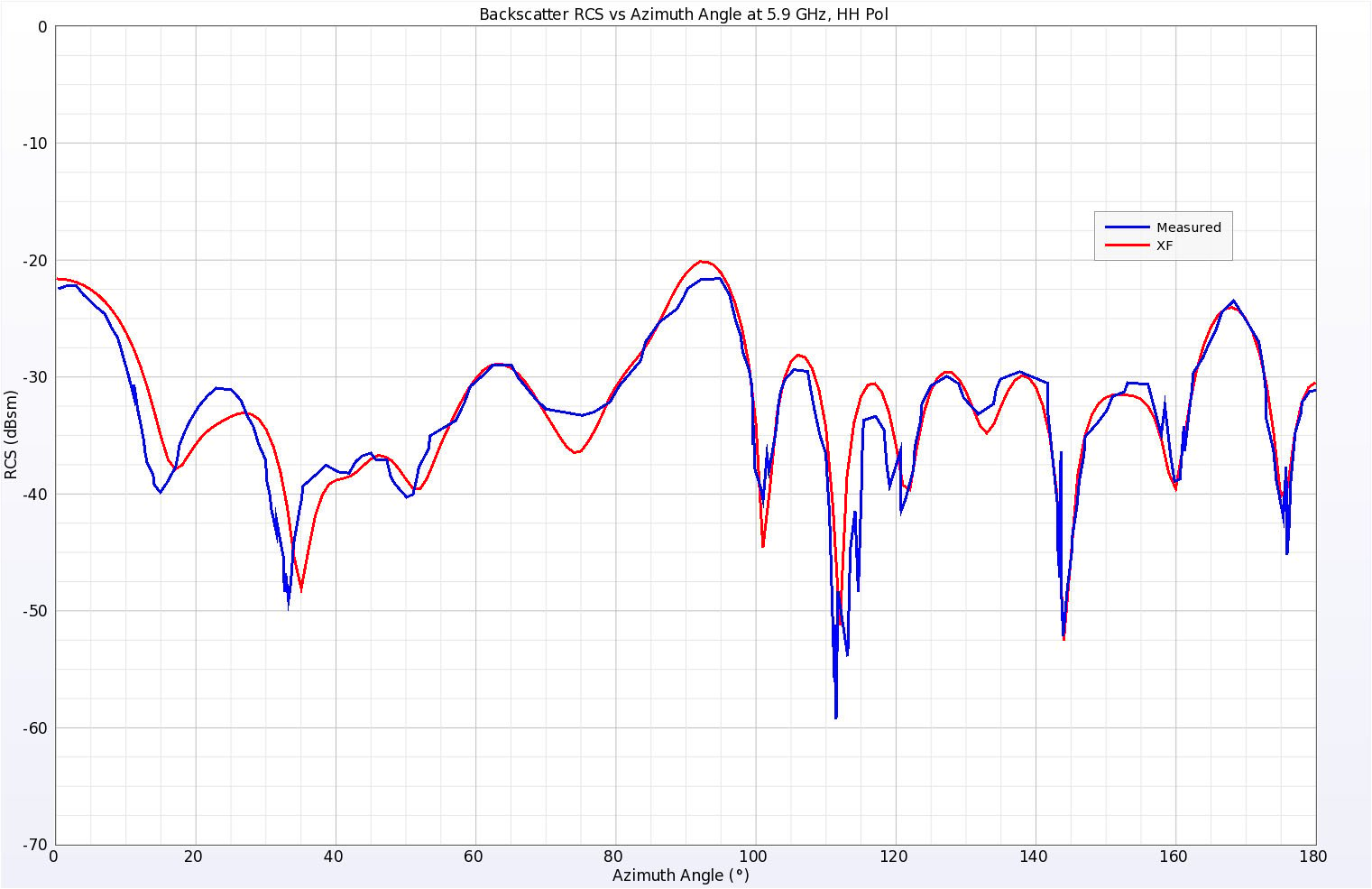
Abbildung 11: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für den Plate Cylinder bei 5,9 GHz, horizontale Polarisation.
Die Keil-Platte-Zylinder-Geometrie schließlich kombiniert die drei Strukturen, wobei sich der Scheitelpunkt des Keils im 0-Grad-Punkt und der Mittelpunkt des Halbkreises bei 180 Grad befindet. Die simulierten und gemessenen Ergebnisse zeigen erneut eine gute Übereinstimmung, wie in den Abbildungen 12 und 13 zu sehen ist.
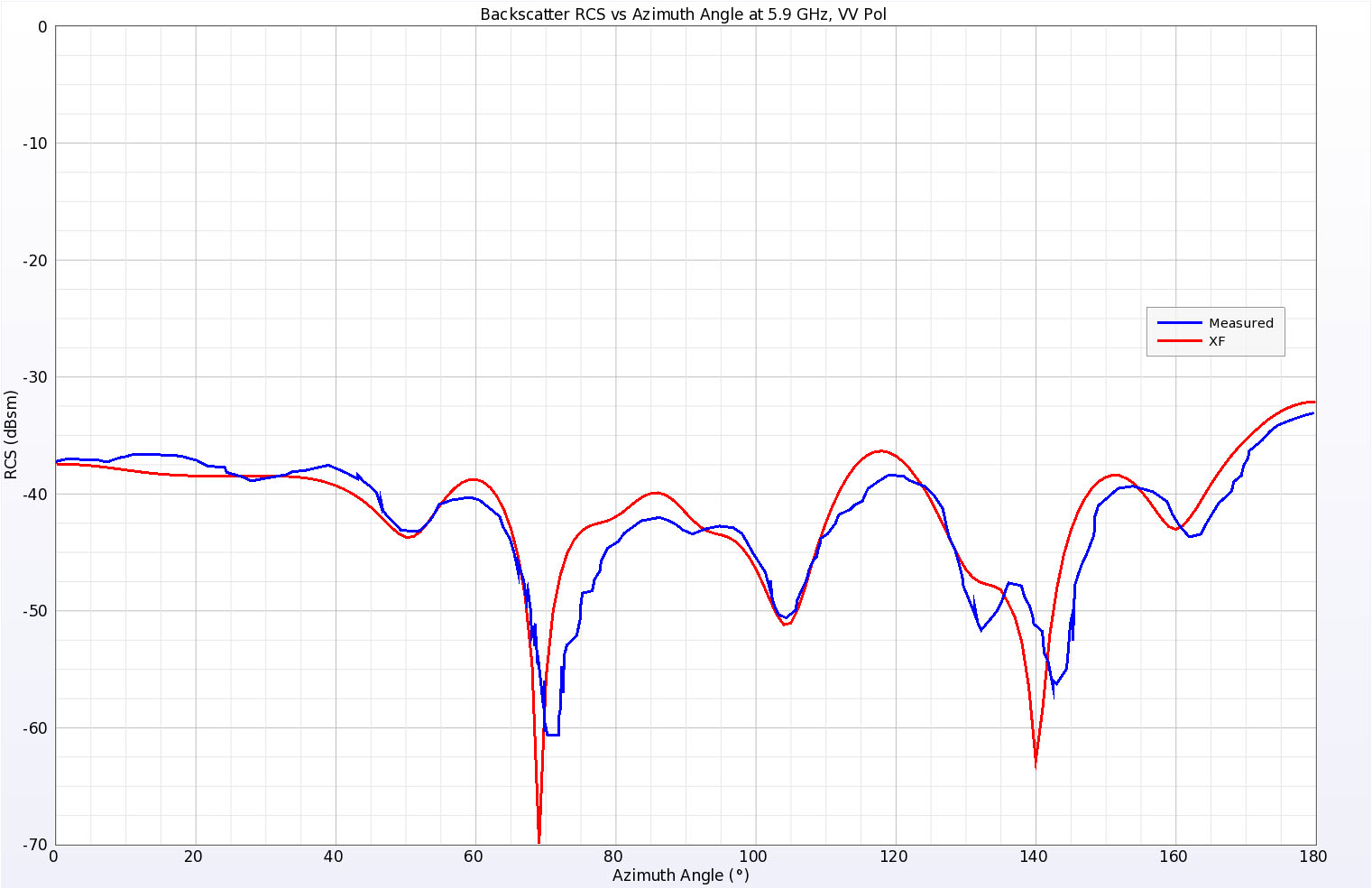
Abbildung 12: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für den Keilplattenzylinder bei 5,9 GHz, vertikale Polarisation.
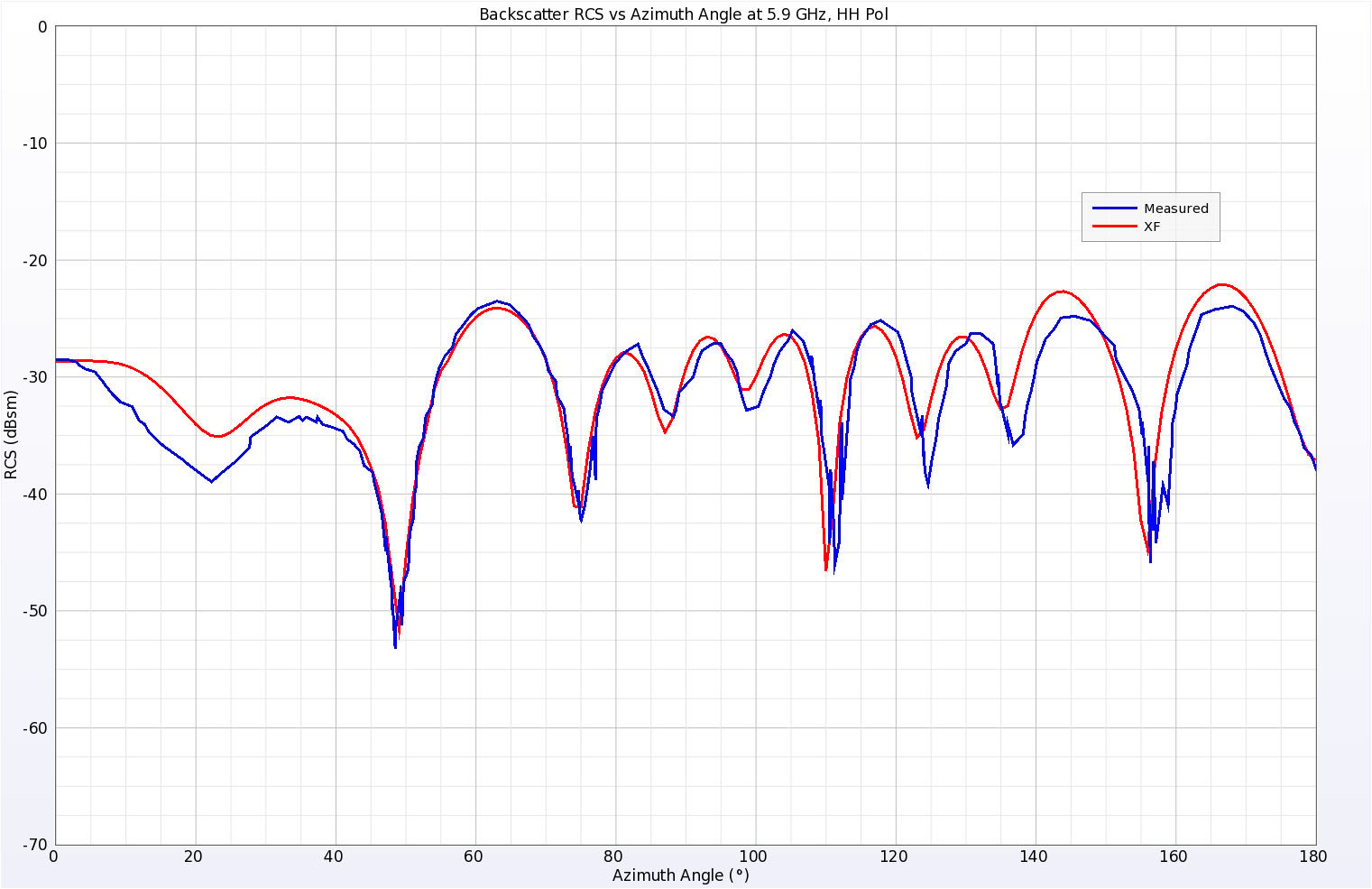
Abbildung 13: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für den Keilplattenzylinder bei 5,9 GHz, horizontale Polarisation.
Erklärungen zu den Zahlen
-
Abbildung 1: Die Geometrie der Visitenkarte: Die X-Länge beträgt 3 Wellenlängen, während die Y-Länge 2 Wellenlängen beträgt (bei 5,9 GHz). Die Dicke beträgt 41 mils.
-
Abbildung 2: Die Geometrie des Keilzylinders: Der Radius des Halbkreises beträgt 1 Wellenlänge, während die Länge der einen Keilseite 2 Wellenlängen beträgt (bei 5,9 GHz). Der Winkel des Keils beträgt 60 Grad, während die Dicke der Platte 41 mils beträgt.
-
Abbildung 3: Die Geometrie des Plattenzylinders: Der Radius des Halbkreises beträgt 1 Wellenlänge, während der Plattenabschnitt 2,5 x 2 Wellenlängen (bei 5,9 GHz) beträgt. Die Dicke der Platte beträgt 41 mils.
-
Abbildung 4: Die Geometrie des Keilplattenzylinders: Der Radius des halbkreisförmigen Teils beträgt 1 Wellenlänge. Der Mittelteil ist eine rechteckige Platte mit 1 x 2 Wellenlängen, während der Keilteil eine Seitenlänge von 2 Wellenlängen hat (bei 5,9 GHz). Der Winkel des Keils beträgt 60 Grad, während die Plattendicke 41 mils beträgt.
-
Abbildung 5: Eine dreidimensionale Ansicht des Keilplatten-Zylinder-Geometrienetzes zur Veranschaulichung der für die Simulationen verwendeten Zellengröße, der Plattendicke und der XACT-Vernetzungsmöglichkeiten.
-
Abbildung 6: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für die Visitenkarte bei 5,9 GHz, vertikale Polarisation. Der Elevationswinkel betrug 10 Grad über der Ebene der Platte und der Azimutwinkel wurde variiert. Null Grad bedeutet normalen Einfall auf eine der kürzeren Seiten der Platte, während 90 Grad normaler Einfall auf eine längere Seite ist.
-
Abbildung 7: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für die Visitenkarte bei 5,9 GHz, horizontale Polarisation. Der Elevationswinkel betrug 10 Grad über der Ebene der Platte und der Azimutwinkel wurde variiert. Null Grad bedeutet normalen Einfall auf eine der kürzeren Seiten der Platte, während 90 Grad normaler Einfall auf eine längere Seite ist.
-
Abbildung 8: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für den Keilzylinder bei 5,9 GHz, vertikale Polarisation. Der Elevationswinkel betrug 10 Grad über der Ebene der Platte und der Azimutwinkel wurde variiert. Null Grad bedeutet normalen Einfall auf den Scheitelpunkt des Keils.
-
Abbildung 9: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für den Keilzylinder bei 5,9 GHz, horizontale Polarisation. Der Elevationswinkel betrug 10 Grad über der Ebene der Platte und der Azimutwinkel wurde variiert. Null Grad bedeutet normalen Einfall auf den Scheitelpunkt des Keils.
-
Abbildung 10: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für den Plattenzylinder bei 5,9 GHz, vertikale Polarisation. Der Elevationswinkel betrug 10 Grad über der Ebene der Platte und der Azimutwinkel wurde variiert. Null Grad entspricht dem normalen Einfall auf die kurze gerade Seite der Platte, während 180 Grad die Mitte des kreisförmigen Randes darstellt.
-
Abbildung 11: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für den Plattenzylinder bei 5,9 GHz, horizontale Polarisation. Der Elevationswinkel betrug 10 Grad über der Ebene der Platte und der Azimutwinkel wurde variiert. Null Grad entspricht dem normalen Einfall auf die kurze gerade Seite der Platte, während 180 Grad die Mitte des kreisförmigen Randes darstellt.
-
Abbildung 12: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für den Keilplattenzylinder bei 5,9 GHz, vertikale Polarisation. Der Elevationswinkel betrug 10 Grad über der Ebene der Platte und der Azimutwinkel wurde variiert. Null Grad entspricht dem normalen Einfall auf den Scheitelpunkt des Keils, während 180 Grad die Mitte des kreisförmigen Randes darstellt.
-
Abbildung 13: Simulierte und gemessene Rückstreu-RCS-Ergebnisse für den Keilplattenzylinder bei 5,9 GHz, horizontale Polarisation. Der Elevationswinkel betrug 10 Grad über der Ebene der Platte und der Azimutwinkel wurde variiert. Null Grad entspricht dem normalen Einfall auf den Scheitelpunkt des Keils, während 180 Grad die Mitte des kreisförmigen Randes darstellt.
Referenzen
-
H. T. G. Wang, M. L. Sanders, A. C. Woo, und M. J. Schuh. "Radar Cross Section Measurement Data, Electromagnetic Code Consortium Benchmark Targets". NWC TM 6985, Mai 1991.
-
A. C. Woo, H. T.G. Wang, M. J. Schuh, und M. L. Sanders. "Benchmark Plate Radar Targets for the Validation of Computational Electromagnetics Programs". IEEE Antennas and Propagation Magazine, Bd. 34, Nr. 6, Dezember 1992.
