Die Geometrie dieses Touchscreen-Beispiels ist der Referenz [1] entnommen und besteht aus drei Antriebselektroden in der XY-Ebene bei z = 0 und vier Sensorelektroden in der XY-Ebene bei z = 254 μm. Die in Abbildung 1 gezeigte Struktur wird in XFdtd mit den integrierten Geometriewerkzeugen erzeugt. Eine der Linien wird zunächst mit einem 2D-Plattenkörper erstellt, die anderen identischen Linien werden dann durch Kopieren, Einfügen und Verschieben erstellt. Nachdem die Geometrie erstellt wurde, wird für die Elektroden eine Leitfähigkeit von 1x10^4 und für das obere, mittlere und untere Substrat eine Dielektrizitätskonstante von 7 festgelegt.
Abbildung 1: Touchscreen-Geometrie mit drei Treiberelektroden und vier Sensorelektroden.
Die 7x7-Kapazitätsmatrix des Touchscreens wird mit dem Electrostatic Solver in XF simuliert. Die sieben Elektroden werden identifiziert, indem jeder von ihnen ein statischer Spannungspunkt zugeordnet wird. Die simulierte SPICE-Kapazitätsmatrix für den unbelasteten Fall ist in Tabelle 1 aufgeführt. Die Werte der Eigenkapazität entsprechen den Werten entlang der Diagonalen, während die Werte der gegenseitigen Kapazität die Werte außerhalb der Diagonalen sind.
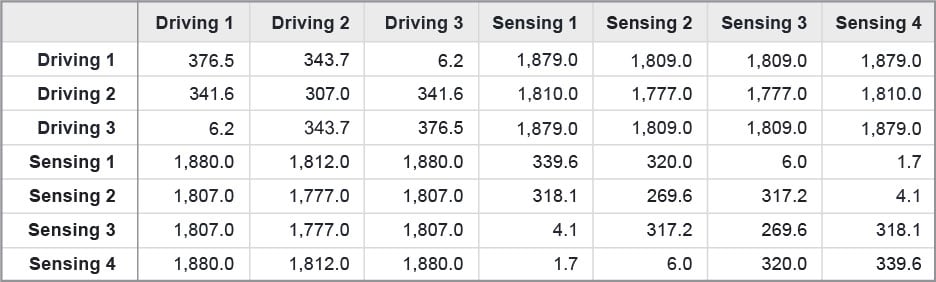
Tabelle 1: Die unbelastete SPICE-Kapazitätsmatrix (fF).
Wenn der Bildschirm geladen wird, ändert sich die Kapazität. In diesem Beispiel wurde ein 1-mm-Stift hinzugefügt und eine statische Spannung von 0 V zugewiesen, um eine Erdung darzustellen. Der Stift berührt den Bildschirm oberhalb des D2S3-Knotens, wie in Abbildung 2 dargestellt. Eine zweite elektrostatische Simulation wurde durchgeführt und die geladene SPICE-Kapazitätsmatrix wurde berechnet. Die Kapazitätsänderung zwischen dem belasteten und dem unbelasteten Fall ist in den Tabellen 2 und 3 dargestellt. In Tabelle 2 ist die gegenseitige Kapazität hervorgehoben, und die Stelle, an der sich der Taststift befindet, ist leicht in Rot zu erkennen, da sie die einzige positive Veränderung darstellt. In Tabelle 3 sind die Werte der Eigenkapazität hervorgehoben. Hier zeigen die negativen Veränderungen die Position des Stiftes an den Elektroden D2 und S3 an.
Abbildung 2: Geerdeter Tastereinsatz am D2S3-Knoten.
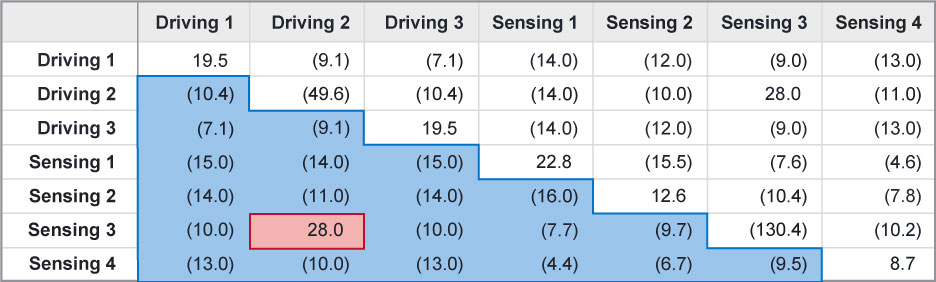
Tabelle 2: Änderung der gegenseitigen Kapazität zwischen belastetem und unbelastetem Fall (fF).
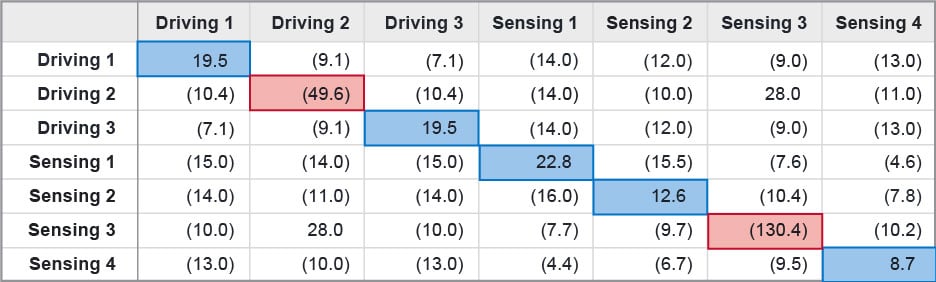
Tabelle 3: Änderung der Eigenkapazität zwischen belastetem und unbelastetem Fall (fF).
Die Spannungsverteilung entlang D2 for ist in Abbildung 3 dargestellt. Der geerdete Taststift hat einen spürbaren Einfluss auf die Spannung und verursacht somit die Kapazitätsänderung.
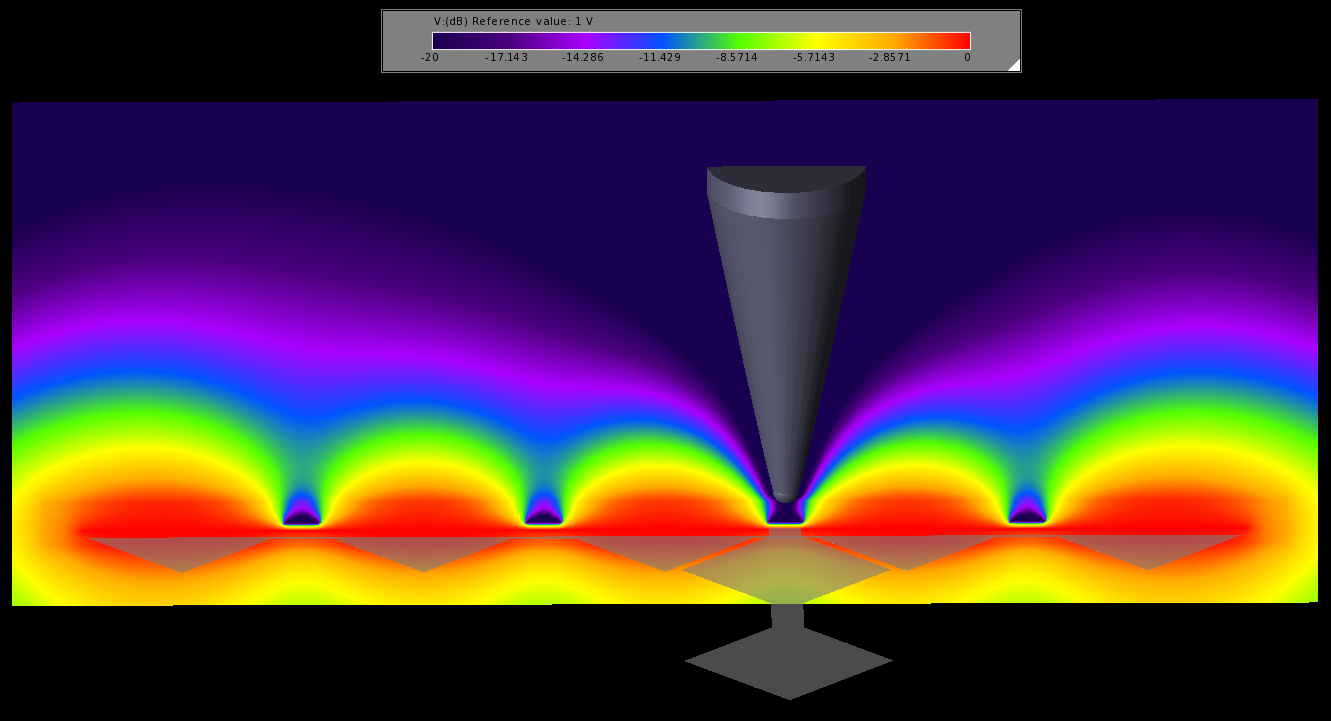
Abbildung 3: Die Spannungsverteilung entlang D2, wenn 1 V an die Elektrode angelegt wird.
Referenz
-
T. H. Hwang et al., "A Highly Areas-Efficient Controller for Capacitive Touch Screen Panel Systems", IEEE Transactions on Consumer Electronics, Vol.56, No.2, pp.1115-1122, Mai 2010.
