- Methoden
- Finite-Difference Time-Domain Methode (FDTD)
Das FDTD Methode für die elektromagnetische Simulation
Der FDTD-Ansatz bietet eine hervorragende Skalierbarkeit der Methode bei wachsender Problemgröße. Wenn die Anzahl der Unbekannten zunimmt, übertrifft der FDTD-Ansatz andere Methoden schnell an Effizienz.
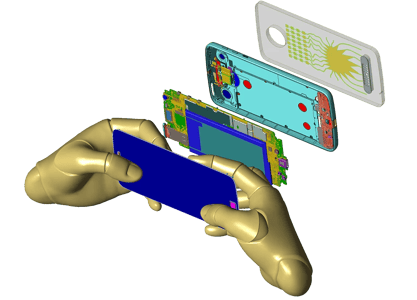
Mobiltelefonmodell mit freundlicher Genehmigung von Motorola Mobility, LLC/Lenovo.
Warum FDTD-Simulationssoftware verwenden?
Während viele elektromagnetische Simulationsverfahren im Frequenzbereich angewendet werden, löst FDTD die Maxwellschen Gleichungen im Zeitbereich. Das bedeutet, dass die Berechnung der elektromagnetischen Feldwerte in diskreten Zeitschritten abläuft. Ein Vorteil des Zeitbereichsansatzes ist die breitbandige Ausgabe bei einer einzigen Programmausführung; der Hauptgrund für die Verwendung des FDTD-Ansatzes ist jedoch die hervorragende Skalierbarkeit der Methode bei wachsender Problemgröße. Wenn die Anzahl der Unbekannten zunimmt, übertrifft der FDTD-Ansatz andere Methoden in Bezug auf die Effizienz schnell. FDTD wurde auch als bevorzugte Methode für die Durchführung elektromagnetischer Simulationen für biologische Effekte von drahtlosen Geräten identifiziert [1]. Es hat sich gezeigt, dass die FDTD-Methode der effizienteste Ansatz ist und genaue Ergebnisse über das Eindringen des Feldes in biologisches Gewebe liefert.
Eine kurze Zusammenfassung - Grundlagen der FDTD-Simulation
Beim FDTD-Ansatz werden sowohl Raum als auch Zeit in diskrete Segmente unterteilt. Der Raum wird in kastenförmige Zellen unterteilt, die im Vergleich zur Wellenlänge klein sind. Die elektrischen Felder befinden sich an den Kanten des Kastens und die magnetischen Felder an den Flächen, wie in Abbildung 1 dargestellt. Diese Anordnung der Felder wird als Yee-Zelle [2, S. 37] bezeichnet und ist die Grundlage für FDTD. Die Zeit wird in kleine Schritte quantisiert, wobei jeder Schritt die Zeit darstellt, die das Feld benötigt, um von einer Zelle zur nächsten zu gelangen. Da die magnetischen Felder räumlich von den elektrischen Feldern versetzt sind, sind auch die Werte des Feldes in Bezug auf die Zeit versetzt. Die elektrischen und magnetischen Felder werden nach einem Sprungschema aktualisiert, bei dem zunächst die elektrischen und dann die magnetischen Felder in jedem Zeitschritt berechnet werden.
Wenn viele FDTD-Zellen miteinander kombiniert werden, um ein dreidimensionales Volumen zu bilden, ist das Ergebnis ein FDTD-Gitter oder -Netz. Jede FDTD-Zelle überlappt Kanten und Flächen mit ihren Nachbarn, so dass jede Zelle vereinbarungsgemäß drei elektrische Felder hat, die an einem ihr zugeordneten gemeinsamen Knoten beginnen. Die elektrischen Felder an den anderen neun Kanten der FDTD-Zelle gehören zu anderen, benachbarten Zellen. Jede Zelle hat auch drei Magnetfelder, die auf den Flächen der Zelle neben dem gemeinsamen Knoten der elektrischen Felder entstehen, wie in Abbildung 1 dargestellt.
Innerhalb des Netzes können Materialien wie Leiter oder Dielektrika hinzugefügt werden, indem die Gleichungen zur Berechnung der Felder an bestimmten Stellen geändert werden. Um z. B. ein perfekt leitendes Drahtsegment zu einer Zellkante hinzuzufügen, kann die Gleichung zur Berechnung des elektrischen Feldes ersetzt werden, indem das Feld einfach auf Null gesetzt wird, da das elektrische Feld in einem perfekten Leiter identisch Null ist. Durch Verbinden zahlreicher Zellränder, die als perfekt leitendes Material definiert sind, kann ein Draht gebildet werden. Die Einführung anderer Materialien oder anderer Konfigurationen wird in ähnlicher Weise gehandhabt, und jedes kann je nach den Eigenschaften des Materials entweder auf das elektrische oder das magnetische Feld angewendet werden. Indem man viele Zellkanten mit Materialien verbindet, kann eine geometrische Struktur innerhalb des FDTD-Gitters gebildet werden, wie z. B. die in Abbildung 2 dargestellte dielektrische Kugel. Jedes kleine Kästchen in der Abbildung stellt eine FDTD-Zelle dar.
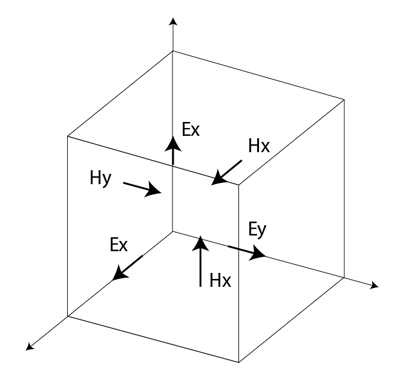
Abbildung 1: Die Yee-Zelle mit beschrifteten Feldkomponenten

Abbildung 2: Eine dielektrische Kugel, wie sie in einem traditionellen FDTD-Gitter mit Treppenstufen vermascht ist. Die einzelnen Zellkanten (Orte des elektrischen Feldes) sind als überlappende Gitterlinien dargestellt.
Die Zellengröße, d. h. die Abmessungen des Kästchens, ist die wichtigste Randbedingung bei jeder FDTD-Simulation, da sie nicht nur die zeitliche Schrittweite, sondern auch die obere Frequenzgrenze für die Berechnung bestimmt. Eine allgemeine Faustregel legt die Mindestauflösung und damit die obere Frequenzgrenze auf zehn Zellen pro Wellenlänge fest. In der Praxis wird die Zellengröße oft kleiner sein, um Abmessungen und Merkmale der zu simulierenden Struktur wie die Dicke eines Substrats oder die Länge eines Drahtes aufzulösen.
Eine Anregung kann auf viele verschiedene Arten auf eine FDTD-Simulation angewendet werden. Eine Methode emuliert die Anregung einer Geometrie an diskreten Stellen, indem eine abgetastete Wellenform auf die Feldaktualisierungsgleichung an einer oder mehreren Stellen angewendet wird. Bei jedem Zeitschritt wird der Wert der Wellenform über diese Zeitspanne zum Feldwert addiert. Die umgebenden Felder verbreiten die eingeführte Wellenform in Abhängigkeit von den Eigenschaften jeder Zelle angemessen im FDTD-Gitter. Eine Berechnung muss solange fortgesetzt werden, bis ein Konvergenzzustand erreicht ist. Dies bedeutet in der Regel, dass alle Feldwerte im Wesentlichen auf Null abgeklungen sind (mindestens 60 dB unter dem Spitzenwert) oder ein stationärer Zustand erreicht wurde.
Fortschritte bei der Zelltreppenbildung
Traditionell gelten treppenförmige FDTD-Zellen als schwerfällig und ineffizient bei der Auflösung von gekrümmten Oberflächen oder stark variierenden Feldern. Fortschritte bei FDTD ermöglichen konforme Netze und die Korrektur von Singularitäten.
Die Yee-Würfelzelle in Abbildung 1 kann im Allgemeinen rechteckig sein. Die Abstände zwischen den Zellen in x-, y- und z-Richtung können im gesamten Problemraum variieren. Dadurch können mehr Zellränder in Regionen mit starken Feldern platziert werden, z. B. in der Nähe von kleinen Merkmalen aus stark leitendem Material. Innerhalb einer Zelle können die Standard-Aktualisierungsgleichungen von FDTD auf vielfältige Weise verfeinert werden, um beispielsweise Drähte zu berücksichtigen, die dünner sind als eine Zellengröße, oder um die starken Felder an den Kanten von Leitern wie Mikrostreifenleitungen zu berechnen. Eine weitere Verfeinerung kann Objekte berücksichtigen, deren Oberfläche die Zelle in beliebigen Winkeln zu den Hauptachsen schneidet. Diese "konformen" Zellen können weiter verfeinert werden, um die Krümmung der Objektoberfläche innerhalb des Volumens der Zelle zu berücksichtigen.
Abbildung 3 zeigt die Geometrie eines Teils eines Mobiltelefons. Zur Verdeutlichung wurde die Sichtbarkeit vieler Teile, einschließlich des äußeren Gehäuses, ausgeschaltet, um den Bereich in der Nähe der Antenne zu zeigen. Ein kleiner Teil des FDTD-Netzes des Telefons ist in Abbildung 4a unter Verwendung einfacher rechteckiger Zellen dargestellt. In Abbildung 4b ist derselbe Teil des Telefonnetzes dargestellt, diesmal unter Verwendung einer Art von konformer Behandlung für Zellen, die Teile der Oberfläche eines Objekts enthalten. Abbildung 5 zeigt eine größere Ansicht der Oberflächen des konformen Netzes.
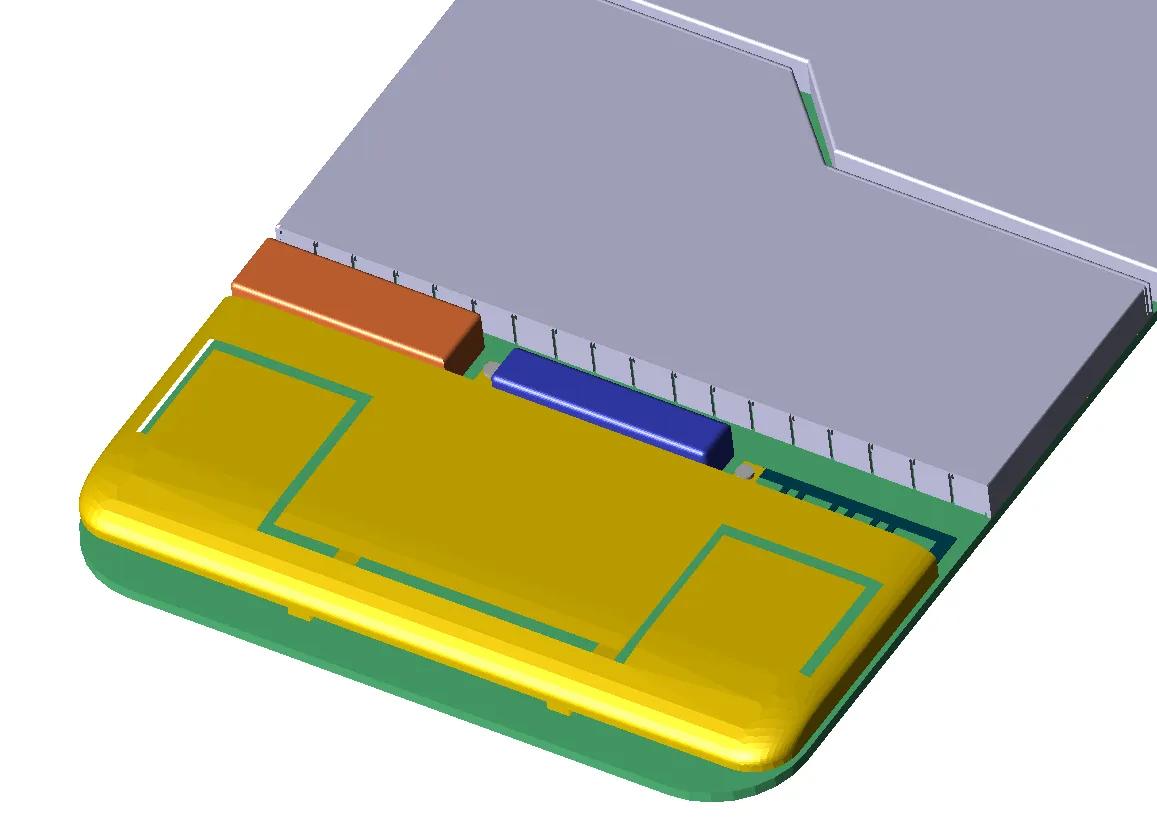
Abbildung 3: Antennenabschnitt eines Mobiltelefons.
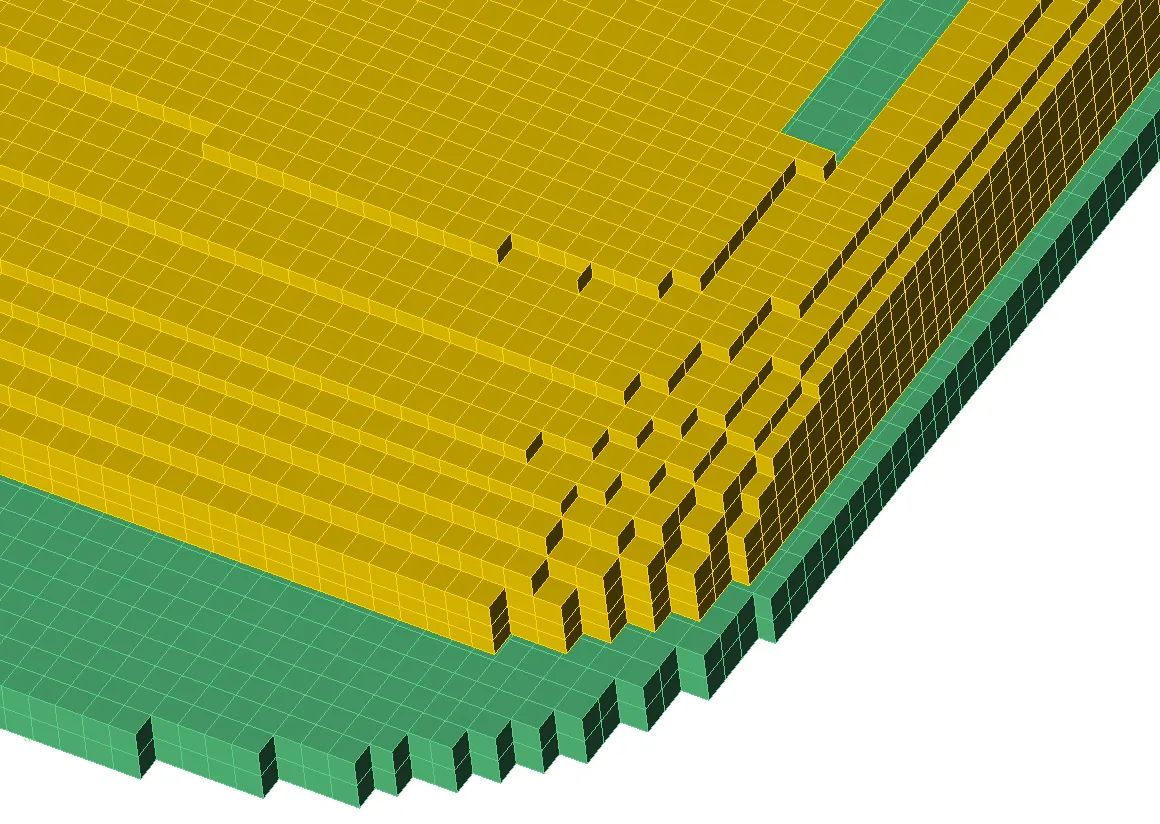
Abbildung 4a: Netzansicht der Antennenecke unter Verwendung eines einfachen rechteckigen Netzes.

Abbildung 4b: Netzansicht einer Antennenecke mit konformem Netz.
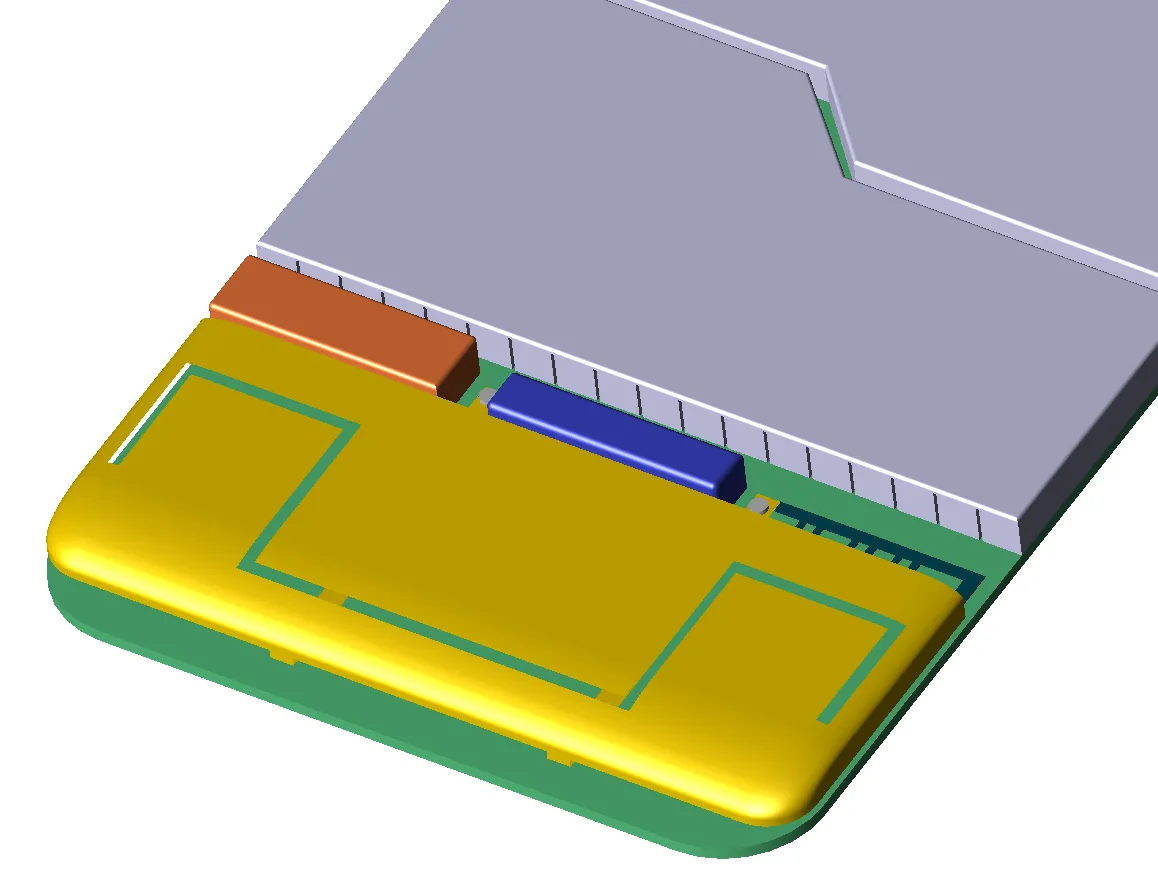
Abbildung 5: Konformes Netz einer Mobiltelefonantenne.
Materialien
Mit FDTD-Simulationssoftware kann eine Vielzahl von elektrischen und magnetischen Materialien simuliert werden. Das einfachste Material ist natürlich der freie Raum. Alle FDTD-Zellen werden als freier Raum initialisiert, und die Felder an allen Zellkanten werden anhand der Gleichungen für den freien Raum aktualisiert, es sei denn, es wird ein anderes Material hinzugefügt, das den freien Raum ersetzt.
Perfekt leitende elektrische und magnetische Materialien werden simuliert, indem das elektrische oder magnetische Feld für alle Zellränder innerhalb dieser Materialien auf Null gesetzt wird. Wegen der Einfachheit der Berechnung für diese Materialien ist es besser, wann immer es möglich ist, einen perfekten Leiter statt eines realen Leiters zu verwenden. Leiter wie Kupfer können in FDTD simuliert werden, aber da die Gleichungen zur Berechnung der Felder in Kupfermaterial komplizierter sind als die für einen perfekten Leiter, dauert die Berechnung länger. In Fällen, in denen nur ein kleiner Prozentsatz der FDTD-Zellen als Leiter definiert ist, ist der Unterschied in der Ausführungszeit natürlich kaum spürbar.
Frequenzunabhängige dielektrische und magnetische Materialien werden durch ihre konstitutiven Parameter der relativen Dielektrizitätskonstante und der Leitfähigkeit oder des Verlustfaktors für das elektrische Material bzw. der relativen Permeabilität und der magnetischen Leitfähigkeit für das magnetische Material definiert. In vielen Fällen sind diese Materialien selbst bei Breitbandberechnungen geeignet, da sich die Parameter über den Frequenzbereich nicht wesentlich ändern.
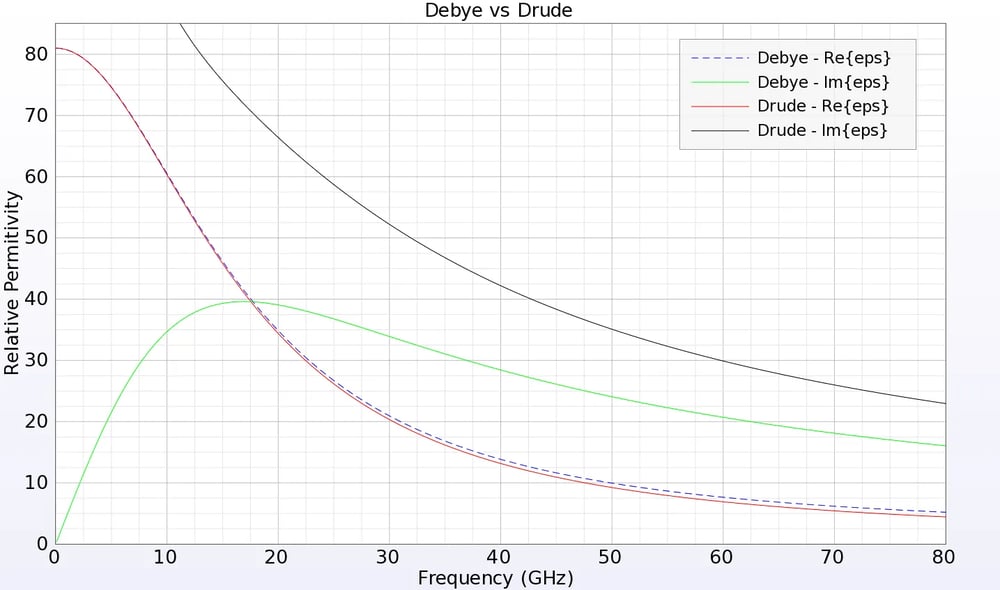
In einigen Fällen ist ein frequenzunabhängiges Material nicht geeignet, und stattdessen sollte ein frequenzabhängiges oder dispersives Material verwendet werden. Einige gängige Beispiele für frequenzabhängige Materialien sind Materialien mit hohem Wassergehalt wie menschliches Gewebe, Metalle, die bei optischen Frequenzen angeregt werden, und Dielektrika über große Bandbreiten. XFdtd bietet die Möglichkeit, elektrische und magnetische Debye- und Drude-Materialien wie Plasmen, Lorentz-Materialien und anisotrope magnetische Ferrite sowie frequenzunabhängige anisotrope Dielektrika zu simulieren. Diese Materialien können Permittivitäten oder Permeabilitäten haben, die bei einigen Frequenzen negativ sind, wodurch sie sich für die makroskopische Simulation von Metamaterialien eignen. FDTD ist auch besonders effektiv bei der Simulation nichtlinearer Materialien, von denen mehrere in XFdtd enthalten sind.
Nahzone vs. Fernzone
Für eine bestimmte Berechnung wird die Geometrie der zu simulierenden Struktur definiert, indem die Zellränder an bestimmten Stellen auf bestimmte Materialien eingestellt werden. Der gesamte FDTD-Geometrieraum, der gemeinhin als Gitter oder Netz bezeichnet wird, setzt sich aus einem dreidimensionalen Block dieser Zellen zusammen. Dieses dreidimensionale Volumen wird bei FDTD im Hinblick auf die Datenspeicherung als Nahzonenbereich betrachtet. Der Feldwert an einer beliebigen Kante des FDTD-Gitters kann als Funktion der Zeit beobachtet werden, indem ein "near-zone"-Punkt in XFdtd gespeichert wird. Andere Datentypen wie stationäre Feldstärken, spezifische Absorptionsraten, S-Parameter oder Impedanz können ebenfalls für geeignete Punkte, Oberflächen und Volumina innerhalb des Gitters gespeichert werden.
Es ist möglich, ein FDTD-Gitter zu erstellen, das groß genug ist, um die Abtastung von Punkten im Fernfeld einer Geometrie zu ermöglichen. In der Regel ist dies jedoch extrem kostspielig in Bezug auf den Computerspeicher und die Rechenzeit, da die Anzahl der Unbekannten (Zellen) höchstwahrscheinlich sehr groß sein wird. Beachten Sie, dass jede FDTD-Zelle eine maximale Größe von einem Zehntel einer Wellenlänge hat, so dass die Bewegung vieler Wellenlängen von einer Struktur eine große Anzahl von Zellen erfordert. In den meisten Fällen ist dies keine geeignete Methode zur Überwachung der Fernfeldergebnisse.
Eine praktischere Methode zur Transformation von Feldwerten in die Fernzone und zur Berechnung von Strahlungsverstärkungen oder Radarstreuungsmustern besteht darin, eine Transformation zu verwenden, um die Nahzonenwerte im FDTD-Gitter in einen Fernfeldwert an einem Ort außerhalb des Gitters umzuwandeln. Dazu wird die Geometrie in einen Kasten eingeschlossen und die Felder auf den Außenflächen dieses Kastens für allgemeine Fernzonenprobleme gespeichert. Die Flächen des Kastens befinden sich fünf FDTD-Zellen von jedem äußeren Rand des FDTD-Gitters entfernt. Damit die Transformation gültig ist, müssen sich alle Teile der FDTD-Geometrie innerhalb des Kastens befinden.
Das in XFdtd verwendete Polarkoordinatensystem ist so definiert, dass sich der Azimutalwinkel (phi) auf die x-Achse und der Elevationswinkel (theta) auf die z-Achse bezieht, wie in Abbildung 6 dargestellt. Dieses Koordinatensystem wird zur Lokalisierung von Fernzonenpositionen und zur Definition der Richtung der einfallenden ebenen Wellen verwendet.
.webp?width=269&height=254&name=image-asset%20(4).webp)
Abbildung 6: Polarkoordinatensystem, das für die Richtungen der Fernzone und der einfallenden ebenen Wellen verwendet wird.
Breitband- und Steady-State-Berechnungen
Im Allgemeinen wird mit FDTD eine Breitbandberechnung durchgeführt, da eine einzige Berechnung Ergebnisse für einen großen Frequenzbereich liefern kann, ohne dass zusätzliche Computerressourcen erforderlich sind. Wenn Daten bei bestimmten Frequenzen benötigt werden, können aus der Breitbandberechnung mittels einer Fourier-Transformation stationäre Daten berechnet werden.
Gängige Beispiele für frequenzabhängige Daten sind Antennenmuster bei bestimmten Frequenzen, biologische Anwendungen wie die spezifische Absorptionsrate (SAR), elektrische und magnetische Feldstärken, magnetische Flussstärken, Leitungsströme und "schaltungstechnische" Informationen wie S-Parameter, Gruppenlaufzeit, Impedanz, Leistung, Effizienz usw.
Sinusförmige Erregung kann in bestimmten Fällen erwünscht sein, z. B. wenn eine starke Resonanz in der Nähe, aber außerhalb des interessierenden Frequenzbereichs vermieden werden soll.
Äußere Grenzen der Strahlung
Ein dreidimensionales Zellengitter bildet die FDTD-Geometrie, und die an jedem Zellenort aktualisierten Felder sind von den benachbarten Feldern abhängig. Aufgrund von Speicherbeschränkungen muss das Gitter jedoch an einem bestimmten Punkt enden, weshalb die Felder an den äußeren Rändern des Gitters nicht korrekt aktualisiert werden können. Um diese Situation zu korrigieren, werden an den Rändern des FDTD-Gitters äußere Strahlungs-Randbedingungen angewendet.
Die äußere Strahlungsgrenze ist eine Methode zur Absorption von Feldern, die sich vom FDTD-Gitter in Richtung der Grenze ausbreiten. Durch die Absorption dieser Felder scheint sich das Gitter unendlich auszudehnen. Die Leistung der äußeren Begrenzungen ist ein wichtiger Faktor für die Genauigkeit einer FDTD-Berechnung, und es sollte darauf geachtet werden, dass sie korrekt verwendet werden.
In manchen Fällen ist eine reflektierende Grenze einer absorbierenden vorzuziehen. Eine perfekt leitende Randbedingung (entweder elektrisch oder magnetisch) kann zur Abbildung der Felder in einer FDTD-Berechnung verwendet werden, um die Symmetrien des Problems zu nutzen. Eine periodische Randbedingung ist nützlich für die Simulation einer einzelnen Einheitszelle einer großen symmetrischen Geometrie.
Computer-Ressourcen
FDTD ist eine rechenintensive Methode, und für die meisten sinnvollen Berechnungen werden ein schneller Computer und mindestens einige Gigabyte Speicherplatz benötigt. Für die meisten Anwendungen ist es recht einfach, den für eine Berechnung erforderlichen Computerspeicher abzuschätzen. Der wichtigste Faktor für den Speicherbedarf und zu einem großen Teil auch für die Laufzeit ist die Anzahl der FDTD-Zellen, die zur Darstellung der zu prüfenden Struktur verwendet werden. Jeder FDTD-Zelle sind sechs Feldwerte zugeordnet: drei elektrische Felder und drei magnetische Felder. Außerdem sind jeder Zelle sechs Flaggen zugeordnet, die den Materialtyp an jeder der sechs Feldpositionen angeben. Die Feldwerte sind reelle Zahlen mit einer Länge von jeweils vier Byte, während die Flags jeweils ein Byte lang sein können. Daraus ergibt sich ein Speicherbedarf pro FDTD-Zelle von 24 Byte für die Felder und 6 Byte für die Flags, insgesamt also 30 Byte. Um den Gesamtspeicherbedarf in Bytes zu schätzen, multipliziert man einfach die Anzahl der FDTD-Zellen mit dem Wert von 30 Bytes pro Zelle. Bei der Berechnung entsteht ein gewisser Overhead, der jedoch im Allgemeinen recht gering ist. Eine bemerkenswerte Ausnahme sind die Breitband-Fernzonenwinkel, die sechs eindimensionale Realwert-Arrays pro Richtung zuweisen.
Die Schätzung der Ausführungszeit einer FDTD-Berechnung ist komplizierter, da die Leistung der Computerprozessoren variiert. Eine Methode zur Schätzung besteht darin, die Gesamtzahl der auszuführenden Operationen zu berechnen. Während der FDTD-Berechnungen gibt es etwa 80 Operationen pro Zelle und Zeitschritt. Die Gesamtzahl der Operationen ergibt sich aus dem Produkt aus der Anzahl der Zellen, der Anzahl der Zeitschritte und dem Faktor von 80 Operationen pro Zelle und Zeitschritt.
Wenn ein Wert für die Fließkommaleistung des Prozessors bekannt ist, kann ein Wert für die Ausführungszeit berechnet werden. Im Allgemeinen besteht jedoch eine bessere Schätzmethode darin, die Ausführungszeit eines einfachen Problems auf einem bestimmten Computer zu bestimmen und dann die Zeit durch das Verhältnis der Anzahl der Operationen zwischen der gewünschten Berechnung und der einfachen zu skalieren.
Es gibt viele Möglichkeiten, die Berechnungsgeschwindigkeit von FDTD zu erhöhen, auch wenn einige einen erheblichen Programmieraufwand erfordern. Einige der effektivsten sind die parallele Nutzung mehrerer CPUs eines Computers, die parallele Nutzung mehrerer Computer, die Optimierung von Berechnungsschleifen für den Cache oder die Nutzung paralleler Methoden auf CPUs wie SSE und AVX. FDTD-Software eignet sich besonders gut für die Berechnung auf GPU-Prozessoren, da die Vorstellung, dass viele Zellen eine relativ kleine Anzahl von Aktualisierungsalgorithmen parallel ausführen, gut zu den Methoden passt, die für die Aktualisierung von Videodisplays entwickelt wurden.
Referenzen
-
C95.3.2002, "Recommended Practice for Measurements and Computations with Respect to Human Exposure to Radio Frequency Electromagnetic Fields, 100kHz to 300GHz", IEEE Standards and Coordinating Committee 28 on Non-Ionizing Radiation Hazards, April 2002.
-
K. S. Kunz und R. J. Luebbers, "The Finite Difference Time Domain Method for Electromagnetics", Boca Raton, FL: CRC Press, 1993.

Webinare
Simulation der Nutzung von LEO-Satelliten zur Ausweitung der NB-IoT-Abdeckung auf ländliche Gebiete
In diesem Vortrag stellt Remcom die Ergebnisse einer Studie vor, die mit Hilfe der Wireless InSite® Raytracing-Simulationssoftware vorhersagt, wie die terrestrische 5G-Abdeckung durch eine LEO-Satellitenverbindung ergänzt werden könnte, um die NB-IoT-Abdeckung in ländlichen Gebieten zu verbessern.
Erkunden Sie Ressourcen
Veröffentlichungen
Was ist neu in XFdtd®?
XFdtd Release 7.11.1 führt mehrere Verbesserungen ein, die die Simulationsgenauigkeit erhöhen, die Analysemöglichkeiten erweitern und den technischen Arbeitsablauf rationalisieren. Diese Version spiegelt Remcoms kontinuierlichen Fokus auf die Lösung hochwertiger Herausforderungen im Antennendesign, der PCB-Modellierung und der Entwicklung von Phased-Array-Systemen wider.
Erkunden Sie Ressourcen
Webinare
Modellierung und Simulation von dynamischen RF-Szenarien mit zeitbasierter Mobilität
Schalten Sie ein, um einen detaillierten Einblick in die Modellierung dynamischer RF-Umgebungen mit Wireless InSite, einer leistungsstarken Plattform für drahtlose Vorhersage und Simulation, zu erhalten. Die Zuschauer erfahren, wie sie die Bewegung von Sende- und Empfangsgeräten, Antennen und Objekten in benutzerdefinierten Szenen simulieren können, die Anwendungen von terrestrischen Kommunikationssystemen bis hin zu Mondmissionen unterstützen.
Erkunden Sie RessourcenSparen Sie Zeit und reduzieren Sie Kosten.
Wenden Sie sich noch heute an Remcom, um eine maßgeschneiderte Lösung für Ihre komplexen elektromagnetischen Herausforderungen zu erhalten.
Angebot anfordern